A few days ago, David Richter and I found a projection from 4D to 3D that preserves tetrahedral symmetry, and produces a Zome-like system with six basic directions, and golden ratio length scaling. Today, David somehow derived a quaternion-based mechanism for the projection that produces that system. Here is the critical excerpt from David's email today:
The other thing I was going to mention was about those vertices of the 120-cell. The idea is to think of them as quaternions and then obtain the other sets using quaternion multiplication. For example, start with the 120 vertices of the 600-cell, those having the shapes (2,0,0,0) (8 vertices), (1,1,1,1) (16 vertices), and (0,a,1,b) (96 vertices). Imagining these as quaternions, I suppose we could write them as 2, 1+i+j+k, ia+j+kb, and so on. Now multiply all of these 120 quaternions on the left by the quaternion 1+i. In effect, you can check, you are transforming each vector (w,x,y,z) to the vector (-x+w,x+w,y-z,y+z). If you do this to all the 120 vertices listed above, you will get the vertices of one of the 600-cells inscribed in the dual 120-cell, dilated by some factor. You can use other quaternions to get other 600-cells as well. You can multiply on the right to get the mirror-images.
It turned out to be trivial to implement the "in effect" transformation he mentions in vZome, so I did it. Sure enough, my 4D data set for the 120 cell, which usually renders as our familiar red-yellow-blue friend with icosahedral symmetry, showed up with the new tetrahedral symmetry.
Excited by this, I hastily boned up on my quaternion multiplication (not hard), and started trying other quaternions.
1+i+j+k
was the first one I tried. Lo and behold, out came the usual red-yellow-blue projection again! Next I tried
1-i+j-k
. Same thing! OK, so the important principle must be to drop one of the components. I tried
1+i+j
... and got an edge-first projection with six-fold rotational symmetry!

This projection required five "new" directions in the icosahedral system. Note that the existing "purple" vZome direction is in use. One of the endpoints of the animation loop shows the sixfold symmetry.
Next, I opened the 4D data set for the 24-cell. The result is below. It only needed one "new" direction, colored turquoise here. This is one of the five directions required for the 120-cell projection!
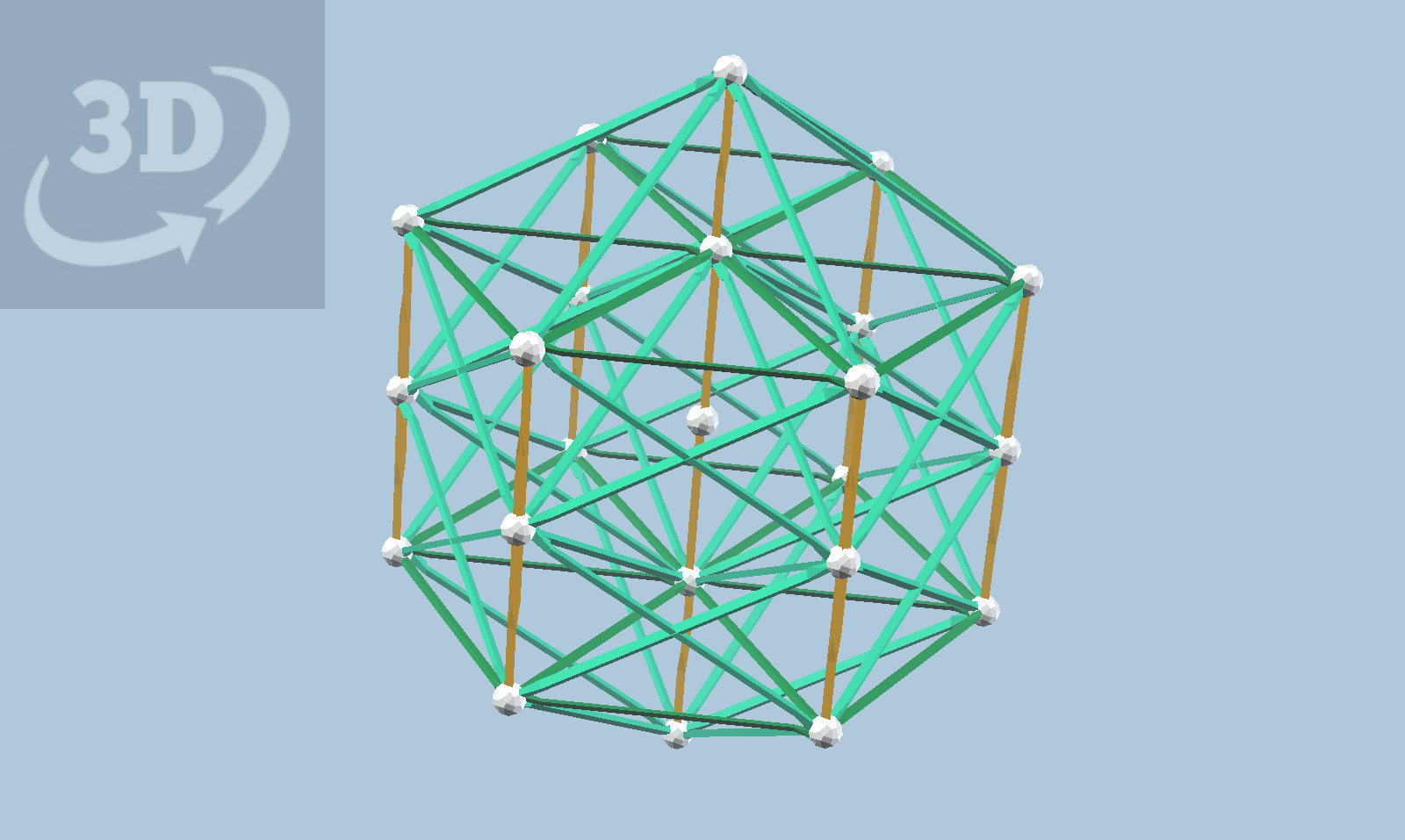
Finally, I opened the 600-cell data set. It also requires the same five new directions. Note that the "maroon" direction from the tetrahedral system makes an appearance. By the way, this is a "face-first" projection of the 600-cell.

There are so many directions to explore. What could be built with this sixfold prismatic system? A model of hexagonal close-packing of spheres? What else? More excitingly, what other symmetry groups, and related "zone" systems, will emerge from using other quaternions? Fivefold prismatic symmetry? Tenfold? Thirtyfold? I suspect that all of the symmetries of H4 are available.
Note that H4 does not actually contain sixfold symmetry. What we see here is threefold rotational symmetry, with mirror symmetry through the orthogonal plane. The 4D polychora we are projecting here have only threefold symmetry, but when projected they exhibit sixfold symmetry, much like the isometric projection of a 3D cube, which produces a hexagonal outline. All these polychora project with a required "central reflection"... just as the tetrahedral projection of the 600 cell has two overlaid tetrahedra at its center, the trigonal projection shown here has two triangles overlaid.
I have a conjecture that the projection preserving fivefold rotational symmetry (face-first for the 120-cell, edge-first for the 600-cell) is easily attainable, using a quaternion that has a factor of tau somewhere in it... something like
1 + tau*i
I'm going to try that shortly. Another quaternion should produce the twofold symmetry. Note that there seem to be "classes" of quaternions (rotations) that will all produce the same projection. This is natural, since there is a great deal of symmetry in H4, and many ways to rotate a model to find an axis with a particular symmetry. I expect that all quaternions that have exactly two coefficients of 1 or -1 and two of zero will produce tetrahedral symmetry... I've already found that k-i produces the same projection as 1+i.
I was right about 1+tau*i! Furthermore, I was correct in my (unstated) prediction that the projection would show pentagons in orange, and be a face-first projection of the 120-cell, and have tenfold symmetry in 3D. Here's an image looking down the only axis of rotational symmetry:

Just as the sixfold system reused maroon from the tetrahedral system, this one reuses lavender and olive from that system. It requires just two new directions, colored here as navy and rose. Both of these are among the five new directions in the sixfold system... typically serendipitous.
The image above is the same 120-cell, now viewed with along a blue axis. Note that the mirror symmetry is not the usual XZ plane... it is through (obviously) the single axis of tenfold symmetry. You can see the two "poles" of the model, to the upper left and lower right. The red edge you are looking straight at is a joint between two adjacent flat dodecahedra, and there are ten identical ones circling the equator. In this flat dodec, you're seeing the largest Petrie polygon edge-on, seen as a zigzag of rose, lavender, and blue struts.
Now you, too, can play with quaternion multiplication! Modern vZome includes a tool for generating 4D polytopes, with optional quaternion multiplication applied before projecting to 3D. I've recorded a short YouTube video explaining how to use it.